Beneath the Hood: Exploring the Architecture of Levva’s Smart Solvers for sUSDe Yield Farming

In a previous article, we introduced Levva’s innovative DeFi component–smart adapters, also known as solvers, which are capable of calculating optimal swap routes between input and output tokens. Solvers are key to enhancing yield farming strategies, particularly for assets like Ethena’s sUSDe. 

In this article, we’ll dive deeper into the architecture of solvers, exploring the technical mechanics of their function using an exchange graph, pathfinding with Dijkstra’s algorithm, and the possibilities of on-chain vs. off-chain implementation.

This one is for all you giga-brains out there.

Constructing the Exchange Graph

At the heart of Levva’s solver architecture is the exchange graph, a dynamic representation of token swaps across supported decentralized exchanges (DEXs).

It is represented by a set of supported assets Ai  i [1, ... ,N] and functions with a set of supported DEXs {Uniswap, Curve, Balancer, Pendle}

 Here’s how it’s built:

Assets as Nodes: Each asset in our set of supported tokens forms a node in the graph. Supported assets include common tokens like WETH, WBTC, and USDC(t), as well as ETH LRTs such as amphrETH and agETH.

Pools as Edges: Each edge represents a liquidity pool that facilitates swaps between two tokens. These edges are weighted by the total cost of swapping, which includes:

• Protocol fees
• Price impact
• An additional overhead cost to account for slippage and MEV (Maximum Extractable Value) manipulation.

Directional Edges: To reflect real-world trading conditions, edges are directional. Swapping asset A for asset B may not have the same cost as swapping asset B for asset A in the same pool.

Graph Sparsity and Anchor Nodes

While a fully connected graph would require N(N−1)/2N(N-1)/2 edges for NN distinct assets, the reality is far more efficient. The graph is sparse, focusing on common use cases such as:

1. Anchor Assets: Lenders primarily provide liquidity in WETH, WBTC, or USDC(t), making these tokens anchor nodes in the graph.
2. LRT Swaps: ETH and BTC LRTs are popular among point farmers and yield farmers, expanding the graph with liquidity pools involving these tokens on Curve and Balancer.
3. Yield Farming with PT Tokens: Farmers often swap ETH, BTC LRTs, or stablecoins for PT tokens on Pendle AMM, adding a critical final layer to the graph.

By tailoring the graph to Levva’s use cases, we reduce computational overhead while ensuring it’s robust enough to handle real-world scenarios.

Finding the Optimal Path with Dijkstra’s Algorithm

Once the exchange graph is constructed, the next challenge is finding the most cost-effective route between two tokens. For this, Levva employs Dijkstra’s algorithm, a widely used method for finding the shortest path in weighted graphs.

How Dijkstra’s Algorithm Works

1. Initialization: Start from the input token node and set the initial cost to 0. All other nodes are initialized with infinite costs.
2. Iterative Updates: At each step, the algorithm:
   • Visits the node with the lowest cumulative cost.
   • Updates the costs for its neighboring nodes based on edge weights.
3. Guaranteed Optimality: Once a node is visited, the path to that node is guaranteed to be the shortest possible.

This process continues until the target node (output token) is reached or all nodes are processed.

Scalability and Efficiency

Using a priority queue (e.g., a binary heap) reduces the algorithm’s time complexity to O((V+E)log⁡V)O((V+E)\log V), where VV is the number of nodes and EE is the number of edges. This ensures that the algorithm scales effectively even with a large number of supported tokens and exchanges.

Building the Exchange Graph in Practice

To construct the exchange graph dynamically, Levva uses tools like Subgraph to query liquidity pool data from supported protocols such as Uniswap, Curve, Balancer, and Camelot. The process includes:

1. Querying Factory Contracts: Identify all pools involving supported assets.
2. Applying Liquidity Thresholds: Backpropagate from high-liquidity pools (e.g., Pendle AMM) to ensure the graph focuses on meaningful paths.
3. Periodic Updates: Reassess connections (pools) and edge weights (costs) regularly to reflect changes in market conditions.

The graph is stored as an edge list and a separate edge weights array, enabling efficient updates and pathfinding.

Off-chain solvers and On-chain routers

One of the key design considerations for Levva’s solvers is whether to operate on-chain or off-chain. While the swap routing algorithm may operate off-chain, our initial on-chain goal is to re-utilize existing router infrastructure of Uniswap, Curve, Balancer, and Pendle and to build our router functionality on top of that. We want to use the above routers and combine asset swapping with Levva position management dynamically based on the best liquidity available at the time of user action. The solver decides what is “best” in this context. Initially, the solver will calculate the route parameters and the sequence of smart-contract calls off-chain and then call Levva router smart-contract. Levva router smart contract, in turn, will handle all of the validity checks and implement router interfaces for the abovementioned protocols.   Ultimately, we will work on decentralizing the solver by looking into the following aspects of its operations: 

• Trust Minimization: The solver/ pathfinder service can run as an Autonomous Verification Service (AVS), decentralizing execution and removing trust assumptions from Levva.
• Decentralization: Further remove trust assumptions by storing the graph, weights, and pathfinding algorithm directly on-chain.

Use Case: Leveraged Yield Farming on sUSDe

Let’s apply this architecture to a practical scenario: swapping USDC for PT sUSDe on Pendle with leverage. Here’s how Levva’s solvers could optimize the route:

1. Borrow USDC from Levva pools.
2. Swap USDC for DAI on Curve’s 3pool.
3. Stake DAI to receive sDAI.
4. Swap sDAI for sUSDe on Curve’s sUSDe pool.
5. Use sUSDe to purchase PT sUSDe on Pendle.

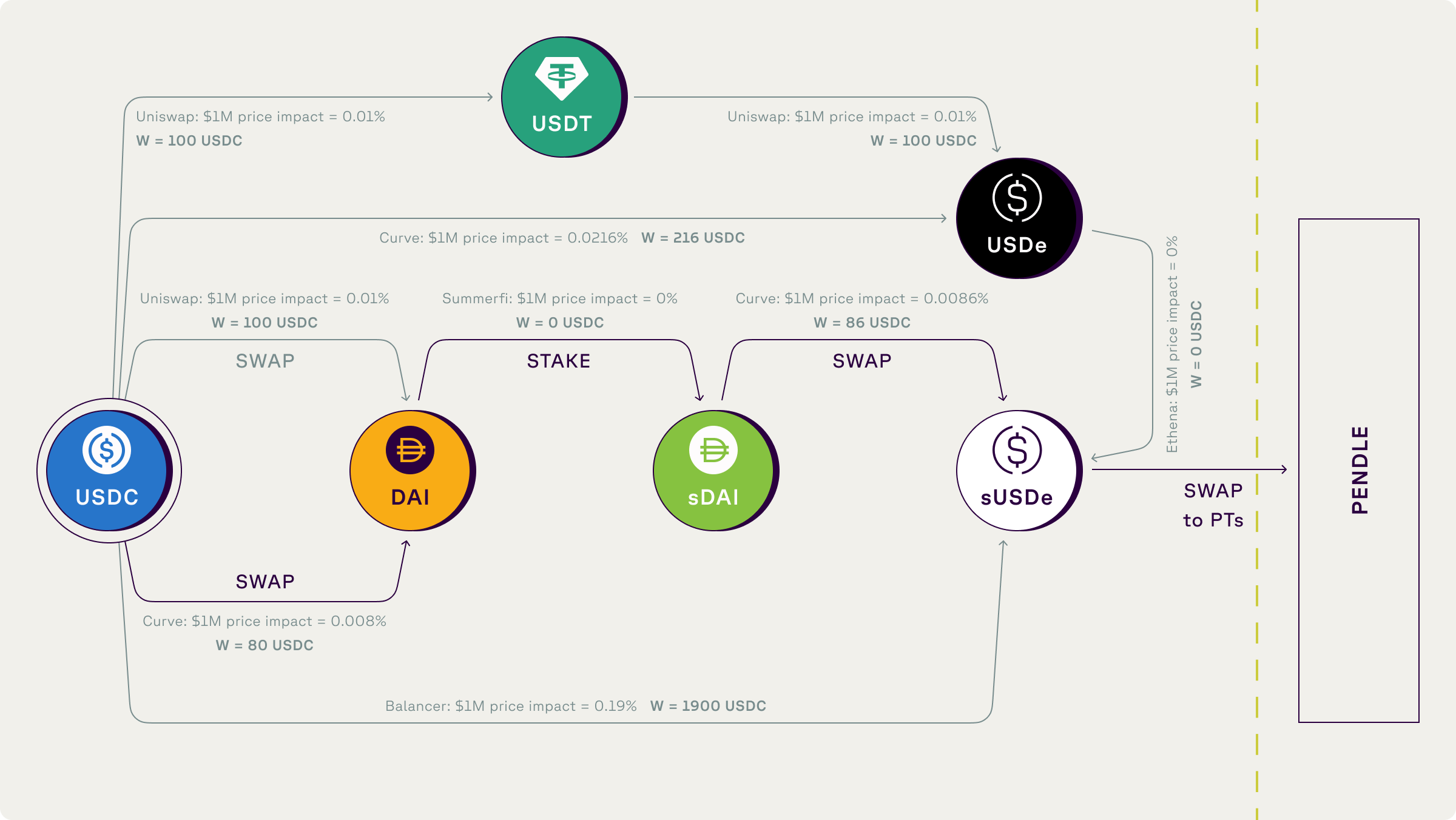
The solver would evaluate multiple routes, minimizing transaction fees, slippage, and protocol commissions. This ensures users achieve the best possible yield with minimal effort.

Conclusion: Optimizing DeFi with Smart Solvers

Levva’s smart solver architecture is designed to simplify complex DeFi operations, making yield farming more efficient and accessible. By constructing an optimized exchange graph, leveraging Dijkstra’s algorithm, and exploring on-chain and off-chain implementations, Levva is creating a system that empowers users to maximize their returns while minimizing risk.

As we continue to test and refine this technology, we’re excited about the potential to fully decentralize solver operations and bring unprecedented efficiency to DeFi. Stay tuned for more updates as Levva pushes the boundaries of what’s possible in DeFi. 🚀